The Making of
High-Precision Optical Flats and Secondary Mirrors
It is assumed that three fairly identical glass blanks have been obtained. If this project is going to be an elliptical flat for a telescope, then the diameter of the blanks should be no smaller than 1.6 times the minor axis. More won't hurt, it'll just cost a little more. To start off, label the sides with an electric pencil so they can be identified. Label one of them A towards one surface, another B towards one surface, and finally, label one of them C towards one surface. Bevel all six edges as you would a telescope mirror blank. Remove any surface flares or labeling extrusions, then grind Center over Center strokes on surfaces A against B, B against C, and C against A with coarse grit, changing which is on top or bottom in roughly 10 minute intervals, until the three are uniformly flat. The amount of time with one above the other should be identical as the amount of time after reversed, and between each pair sets. You can time your sessions, or you can count strokes.
The reasoning of doing three together like this is that they will all three approach flatness, rather than concave or convex. Let's assume that surface A wants to be concave. In order to mate with surface A, surfaces B and C would have to obtain convex shapes. When B and C are ground together, they would rub centers since both are convex. They would eventually grind their centers away. For all three to grind mating surfaces together, only flatness could be the possible shape.
It is recommended that the exact same number of strokes occurs during each session. I do 9 strokes with A on B, then move around the barrel about 1/12 rotation, do 9 strokes, and continue until I have been around the barrel twice. I rewet with new grit and repeat for a total of 4 of these sessions. Then I do B on A the same way. Then C on A, then A on C, then B on C, then C on B. That whole inning takes about an hour, and each part of the session was exactly like any other part.
Once they have been ground flat with 80 grit, the usual process of grinding finer and finer grits is used. Remember, continue to rotate between A&B, B&C, C&A throughout the process, and remember to continue to flip the work over. This process is continued through to 3 micron grit, just as with a telescope mirror. 3 micron may make polishing easier, but increases the probability of scratching. 3 micron will also yield a higher degree of flatness.
You are eventually going to have to look through the glass to examine interference fringes, so if the back sides of these aren’t already polished, they need to be. They do not need to be of optical degree of precision on the backs.
In order for the back side of the glass to not get scratched while working, I paint the yellow for about three coats, then another couple of coats with blue paint on one, gray paint on another, and brown paint on the third [or whatever colors you choose]. This keeps the glass from being scratched. The yellow underneath is an indicator color. If the brown paint gets scratched through and I can see yellow, then I add some more paint. The yellow lets me know that I had gone through a bit. Paint remover, or acetone, when finished will clean them up nicely.
Pour a pitch lap onto a fourth equally sized tool. Equal size is arguable between ATMers. I prefer equivalent laps for working flats. Polish Center over Center strokes onto the first surface. Work for ten minutes, then flip them over and work for ten minutes. Continue until polished. Once the mirror is polished, work another surface. This will give you three flats to figure with clear glass to look through. Laser test the glass to confirm the glass is not under-polished. You can interference test them at any time. The amount of polishing you will be doing to perfect the surfaces will eventually surpass the amount of polishing you will have to do to get a laser-test polish. By the way, if these flats are to be optical windows, this has to be done on the back sides as well, and you can name them a, b and g.
Using Fringes
on Three Flats to Determine How Far Each is from Flat and Which Way
What are fringes? Fringes are the result of constructive and destructive interference. Assume two glasses are perfectly planar, and set together in such a way that they are very close but slightly tilted with respect to each other due to spacers set between them of different thicknesses. The space between them is thin at one side and thick at the other. Between the two ends the glasses separate at a uniform rate. The air space between them has intervals in which the light enters, passes some distance to the other glass, and some of the light reflects back to the first one again. Granted, much of the light passes through, but some does, in fact, reflect back. The light reflecting back from the top of the second glass will interfere with the light reflecting back internally from the bottom of the top glass, either constructively or destructively. When the interference is constructive, the light is fairly bright because the energies are combined. When the interference is destructive, the light is fairly dark because the light waves are eliminating each other. Since the two glasses are planar and tilted, then the regions of equivalent separation are linear perpendicular to the vector in which they are widening. The resultant illusion is that dark bands, or fringes, are formed along the lines of equal thickness where the distance between them is a multiple of 1/2 wave, and the alternate spaces are constructively interfering in which the bands are bright. The bands represent lines of elevation between the two glasses that are in 1/2 wave intervals.
Now, if the glasses are not perfect planes tilted from each other, then the illusion is different. If the two glasses are planar except for a low spot on one of them, then the distance between them at that low spot is now larger than surrounding regions, and the result is that the fringes at that spot will bend in such a way that is in response to the glasses being further apart. The lines of elevation will be similar to regions where the glasses are wider apart, or uphill. The curve of this region will be concave towards the thick gap and convex toward the thin gap. The amount of depression in this low spot can be calculated by counting how many fringes of deviation there are and multiplying by 1/2 wave (550/2 nm). If the fringes bend toward the thin space (concave toward the thick spacer), then there is a low spot. If the fringes bend away from the thin spacer (concave toward the thin spacer), then there is a high spot.
You need to use monochromatic light, light of only 1 wavelength. I select 546.1 nm for two reasons. First, it’s readily available from a mercury lamp. A green filter over a mercury bulb will filter out most wavelengths leaving the green spectrum line of 546.1 nm to pass. Secondly, it’s very near the human center of color perception. Most opticians use 550 nm as their wavelength by which their mirrors are based against, and 546.1 is very close to that.
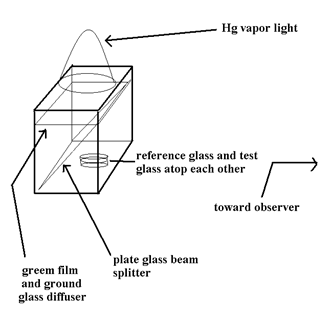
Cellophane used to package CDs, cigarettes, and other commercial material works well for fringe testing for spacing the glasses apart. Saran Wrap also works well, but is stickier and more difficult to move into position. One note regarding cellophane: the news stuff is stickier than the old stuff. It must be a difference composition. The old stuff slides easily, the new stuff doesn’t slide well and it breaks with a little “pop”, messing the whole thing up. Try to find cellophane on something old, like a BGs CD. Cut the cellophane into triangular pieces to place at the perimeter of the glasses. You will find that the three won't all make the same thickness, and there will be fringes. You can peer down onto the glasses and see the fringes, but a direct view is required to make any analysis. This can be done either by a fringe box or a fringe tube. I use a fringe box like Thompson, and I use a fringe tube like Texereau. Both will work. I also set the bottom glass on three blocks directly under the spacers so the bottom glass and the top glass will bend exactly the same as gravity influences them. It is also good if they are the same thickness and material so they will bend identically. Otherwise their difference in bending will show as a difference in fringe shapes.
If you are too close you will see the fringes refracted through the glass, and misinterpretation of their straightness may occur. You either need to get way back, or use an alternate method of observing/recording the fringes. I look or photograph the fringes from many feet away using a fringe box. Others use collimating lenses, like in a Fizeau interferometer.
Once the fringes are seen or photographed, the following can be used to determine the prescription of the glass.
Label the three flats A, B and C.
Fringe test AB to get C#, BC to get A#, and AC to get B#, where A#, B# and C# are the number of fringe differences seen with convex being positive and concave being negative.
A'= C# + B# B' = A# + C# C' = A# + B#
F = ( A' + B' + C') / 4
dA = A' – F, is the number of fringes from flat with convex being positive for A.
dB = B' – F, is the number of fringes from flat with convex being positive for B.
dC = C' – F, is the number of fringes from flat with convex being positive for C.
Example 1:
A, B, and C are tested showing that AC are mating with straight lines, AB are mating with straight lines, and BC are 2 fringes convex.
A# = +2 B# = 0 C# = 0
That means that A' = 0 + 0 = 0 B' = 2 + 0 = 2 C' = 2 + 0 = 2
This makes F = ( 0 + 2 + 2 ) / 4 = 4/4 = +1
This means that
dA = A' - F = 0 - 1 = -1 implying 1 fringe concave from flat for A, 1/2 wave concave.
dB = B' - F = 2 - 1 = +1 implying 1 fringe convex from flat for B, 1/2 wave convex.
dC = C' - F = 2 - 1 = +1 implying 1 fringe convex from flat for C, 1/2 wave convex.
Example 2:
A, B, and C are tested showing that AC are 1 fringe convex, AB are 2 fringes concave, and BC are 7 fringes concave.
A# = -7 B# = +1 C# = -2
That means that A' = +1 - 2 = -1 B' = -7 - 2 = -9 C' = -7 + 1 = -6
This makes F = ( -1 - 9 - 6) / 4 = -16 / 4 = -4
This means that
dA = A' - F = -1 - (-4) = -1 + 4 = 3 implying 3 fringes convex from flat for A, 1.5 waves convex.
dB = B' - F = -9 - (-4) = -9 + 4 = -5 implying 5 fringes concave from flat for B, 2.5 waves concave.
dC = C' - F = -6 - (-4) = -6 + 4 = -2 implying 2 fringes concave from flat for C, 1 wave concave.
Here are some interference patterns and their explanations. The top is the thick gap and the bottom is the thin gap.
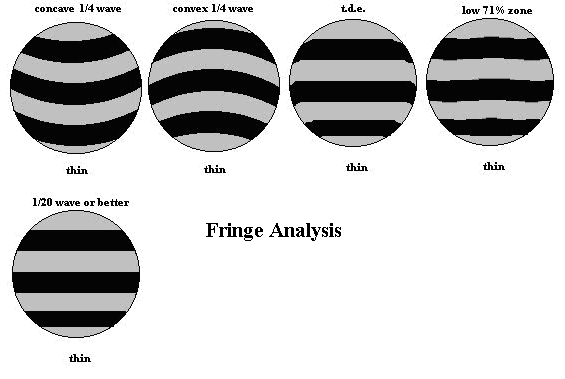
Example 3:
A, B, and C are tested showing that AC are 1/4 fringe convex, AB are 1/5 fringe convex, and BC are 1/4 fringe concave.
A# = -0.25 B# = +0.25 C# = +0.2
That means that A' = 0.25+9.2 = 0.45 B' = -0.25+0.2 = -0.05 C' = -0.25 + 0.25 = 0
This makes F = ( 0.45 - 0.05 + 0 ) / 4 = + 0.1.
This means that
dA = A' - F = 0.45 - 0.1 = 0.35 implying 0.35 fringes convex from flat for A, or 0.17l .
dB = B' - F = -0.05 - 0.1 = -0.05 implying 0.05 fringes concave from flat for B, or 0.025l.
dC = C' - F = 0 - 0.1 = -0.1 implying 0.1 fringes concave from flat for C, or 0.05l.
Correcting
Non-Planar Surfaces
It is most probable that the three test surfaces will not all be planar (flat). It is also most probable that the outer edge is turned down. We will correct the non-planarness, but leave the t.d.e. It will be either removed or unused.
One method: If the glass has been determined to be convex, then the correction stroke will be similar to parabolizing a telescope mirror. If you have a favorite stroke for that, then use it. If not, then use the outer portions of the lap to concentrate the polishing on the inner portions of the glass. Be careful not to striate (microripple) the glass. If the mirror is concave, then work needs to be done in order to lower the outer regions. Concentrating the work on the outer portions of the glass will do. It is very easy to turn the very edge over (t.d.e.) during this period. Use whatever strokes you are used to for pulling back correction on an hyperbolized (over-corrected) mirror.
A better method: Make three laps. One is a normal lap, the second has the groves between the pitch squares widened in the middle area, and the third has the groves between the pitch squares widened in the outer areas. The first lap is for normal polishing. The second one is for working the flat toward convex, fixing one that is concave, and the third is for working the flat toward concave, fixing one that is convex. You simply continue with center over center strokes on all three laps and let the amount of pitch over each area do the fixing.
Using the process above for determining concavity / convexivity, and how far from flat they are, you can judge how long and how hard to work the glass in order to simultaneously pull the three glasses into flatness. That is something that must be learned through experience. However, you can see that if glass A is concave by 1/2 wave, glass B is concave by 1 wave, and glass C is convex by 1/4 wave, then glass A needs work on the outer regions, glass B needs about twice as much work in the outer regions, and glass C needs less work and needs it in the inner regions. Perform the work, and retest the glasses.
Fringe testing shows the shape of the glass, but one more examination is highly recommended. If you have a tests sphere, then you can perform ronchi and null razor tests using the newly made flat to intercept the light path at a 45o angle. This will make a double pass interception which you can compare your null images to. This will easily show ripples, zones and rough spots. If you do a false star examination using this apparatus, it will also show the results of nonflatness. If there is a spherical curve to your flat, then it will show itself as astigmatism in this setup. The fact tht it is a double pass test on the flat and a single pass test on the test sphere will double the intensity of errors on the flat.
Fringes can be determined as straight to about 1/10 of a fringe. Since fringes are 1/2 wave in separation differences, then 1/10 times 1/2 is 1/20 wave. If the fringes appear to be straight when testing a glass against a perfect reference flat, then the glass is at least as perfect as 1/20 wave peak to valley. If two glasses are being tested together, and show 1/20 wave between A and B, 1/20 between B and C, and 1/20 between C and A, then these three glasses are better than 1/20. If one was concave and one was convex, then one of the other matches would be convex on convex or concave on concave, and if the tests there are 1/20 between them, then they must both be about 1/40 wave to add up to 1/20 as worst case pairs using three sets of pairs. Straight lines on all three sets are excellent flats. A point; I make no claim that we are testing these glasses to 1/40l precision.
If the glass is to be cut into a secondary mirror, then it
will be an ellipse. The eccentricity of
the ellipse will be 
, or 0.707. This means
that the length of the optical surface, or the Major axis, will be 
times as long as the
minor axis. This means that the length
of the mirror will be 1.414 times the width.
If the glass is a certain thickness, then the length of the glass needs
to be 1.414 times the width plus the thickness plus 10% that total to prevent
the t.d.e. on the edge of the flat from being used as an optical surface. For example, if the glass is 1" thick
and you are going to make a 6" m.a. secondary mirror, then the glass needs
to be no smaller than ( 6 X 1.414 + 1) X 1.1 = (8.484 + 1)X 1.1 = 9.484 X
1.1" = 10.43”. An 11" blank
would suffice. A 12" blank might be
better but would cost more (negligible when compared to the work you're doing).
Cutting Out the Secondary
Mirror From the Optical Flat
In our shop we cut the glass to shape using a 4” diamond grinding wheel turning at 3500 rpm and a water feed system. This will quickly cut glass cold. Painting the optic keeps your fingers from grinding the debris into the newly made optical surface. Painting the ellipse you are after in a different color allows you to sneak up on the right shape. Keep in mind that the ellipse on the flip side will be in a different position so that when it is in the telescope it will be similar to a Cylinder cut at 45o. Afterward, remove the paint using paint thinner, clean the glass and set it back into your interferometer to check for changes. In the past I have set the glass in plaster at 45o angles and sawn through them. I have as many disasters as successes and do not recommend this method.
When finished, you can use one of the flats to cut out your secondary mirror, one aluminized to use as an autocollimation flat, and one unaluminized to use as a standard flat for fringe testing. Be sure to mark on them which side is “good” and to what degree of precision it’s surface can be claimed. For a fringe testing reference flat, you want extreme surface flatness and smoothness [I recommend RMS evaluation]. For autocollimation testing, I recommend smoothness as your first priority and flatness as a secondary concern since some concavity one way or the other is still acceptable for this purpose if you are doing ronchi or razor testing. For autocollimaton laser Interferometry, it must be smooth AND flat. Also, once you have a good test flat for testing in a fringe box, you may get away without doing the A-B-C cutthroat system and make them one at a time.
Fringe Box
